维基上的解释
矩物理意义矩特征主要表征了图像区域的几何特征,又称为几何矩.其中零阶矩$m_{00}$反映了目标图像的面积,一阶矩反映了目标图像的质心位置,二阶矩又称惯性矩,三阶矩主要表现了目标对其均值分布偏差的一种测度,即扭曲度,四阶矩在统计学中用于描述一个分布的峰态。
理解几何矩
在看OpenCV中Camshift算法的时候不明白他为什么那样求主方向轴及外接矩形的长度和宽度,网上搜来搜去没有关于此的好的解释,找来了其算法实现参考的著名论文Computer Vision Face Tracking For Use in a Perceptual User Interface来看也没有解释,想到这应该是大家都知道的显而易见的结论,只是自己不明白。
后来看着公式突然想明白了,备录下自己的理解,首先列出计算的结论,然后再说下他为什么这样算。
我们先看中心二阶矩的定义:

矩形的半长度$w$,半宽度$l$,和椭圆区域拟合中长轴方向$\theta$的计算如下:
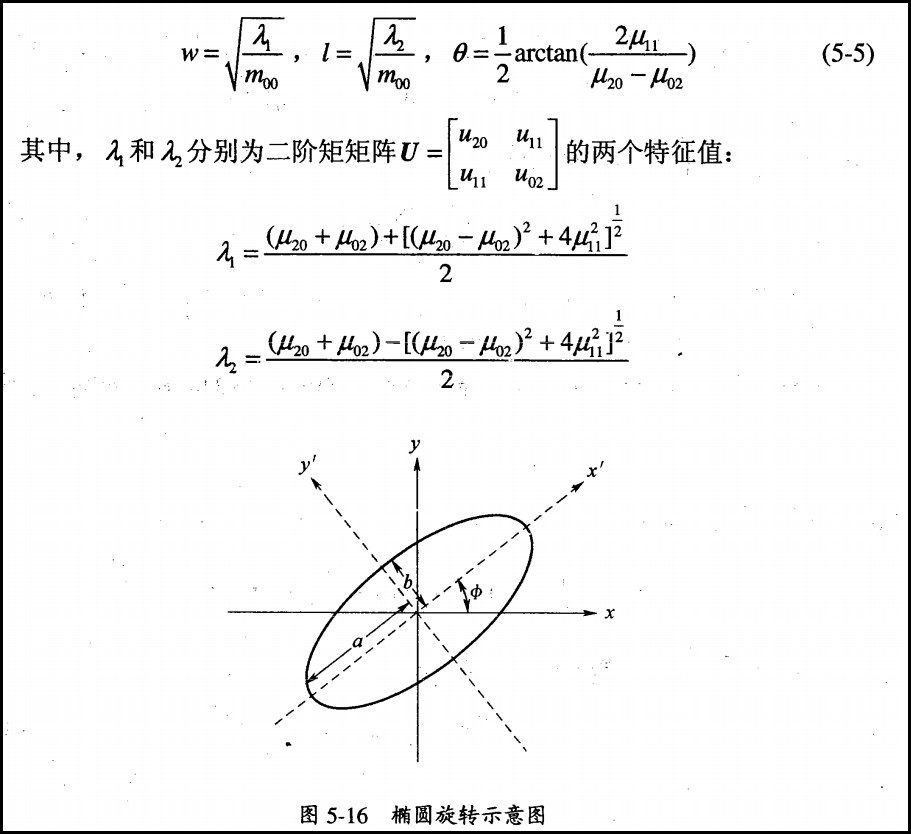

看到这也许不用我解释大家就明白了$\theta$和$w$,$l$为什么那样计算。
但还是啰嗦几句吧,说说自己的直观理解:二阶矩矩阵U左上角为$\sum{x^{2}I(x,y)}$,右下角为$\sum{y^{2}I(x,y)}$,斜对角线为$\sum{xyI(x,y)}$,再看$w$,和$l$的公式,首先看最简单的二阶矩:对角二阶矩,对特征值进行归一化后就相当于只剩下$x^{2},y^{2}$,了,开平方,就是$x,y$,普遍开来,对任意二阶矩,我们想到可以通过坐标变换(旋转$\theta$角度,及主轴的角度)将任意二阶矩变为了对角矩,由$u_{11}^{`}$可以得到$\theta$的值,带入上面的公式容易计算出二阶矩的特征值,将其归一化即得到矩形的长度和宽度值。
以上。
参考文献
[1] 图像局部不变性特征与描述.王永明 王贵锦. 国防工业出版社.




