写在前面
文章整理自模式识别重点实验室的计算机视觉课件,将围绕摄相机成像的几何模型,逐一介绍物体自世界坐标系投射到相机坐标系,相机坐标系投射到图像(物理)坐标系,图像(物理)坐标系投射到像素坐标系的整个过程,还将介绍镜头畸变的一些知识。
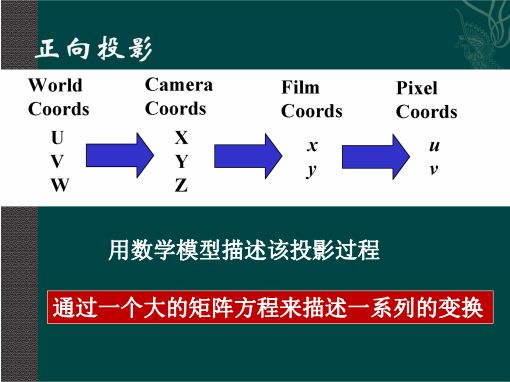
投影过程一览
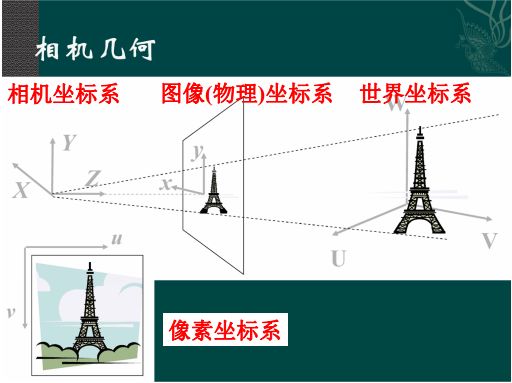
世界坐标系到相机坐标系
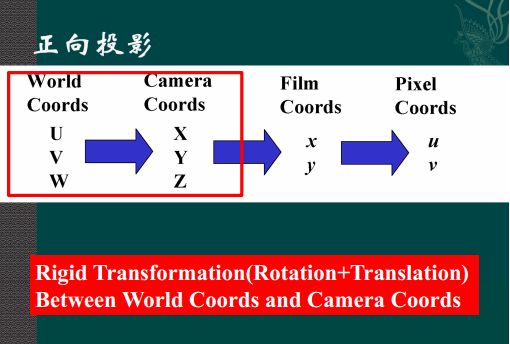

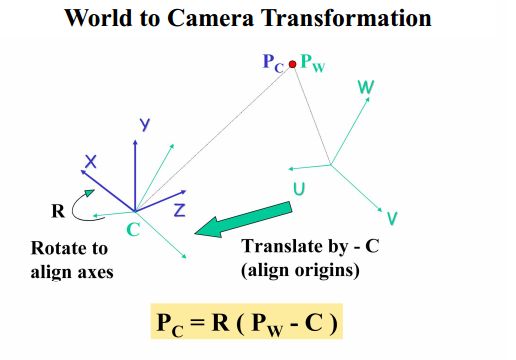

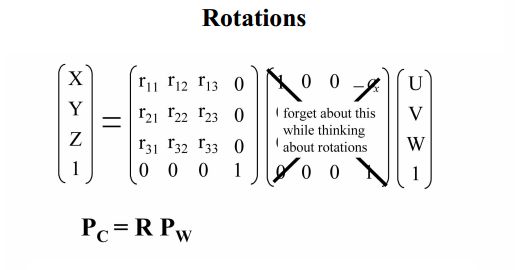
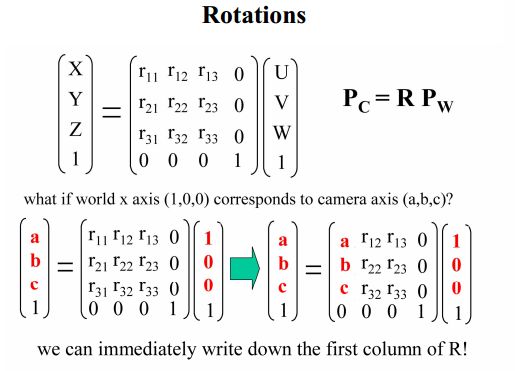
由上图可以看出,世界坐标系下U,V,W单位坐标在相机坐标系下的坐标,依次排成竖排,即为旋转矩阵:
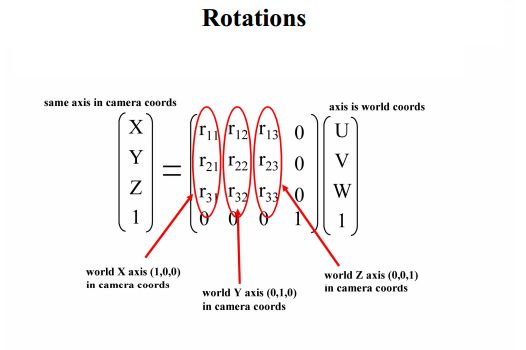
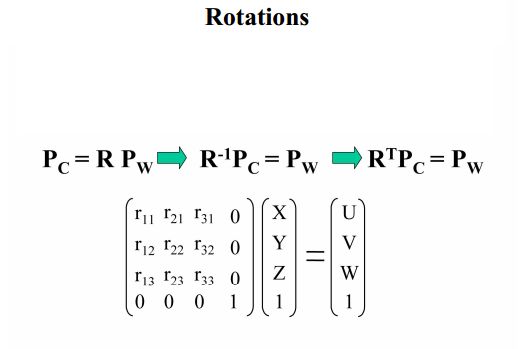
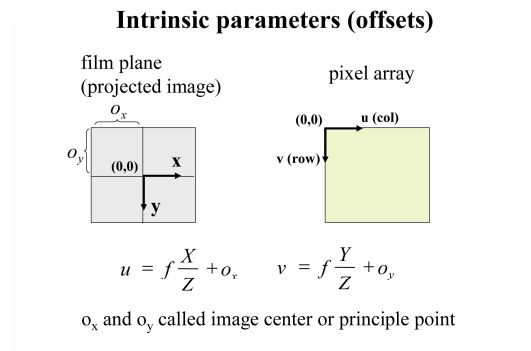
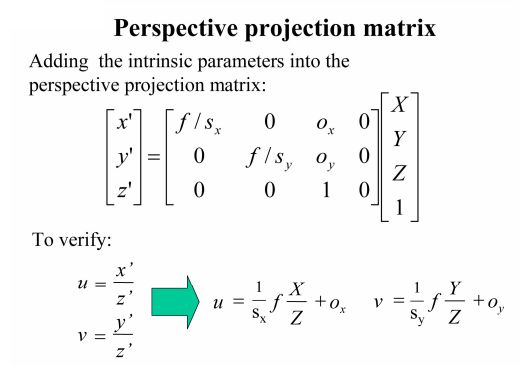
相机坐标系到图像(物理)坐标系
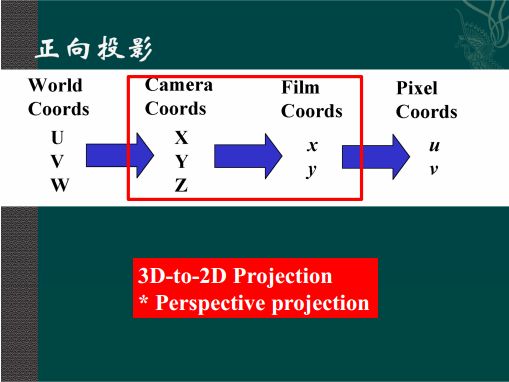
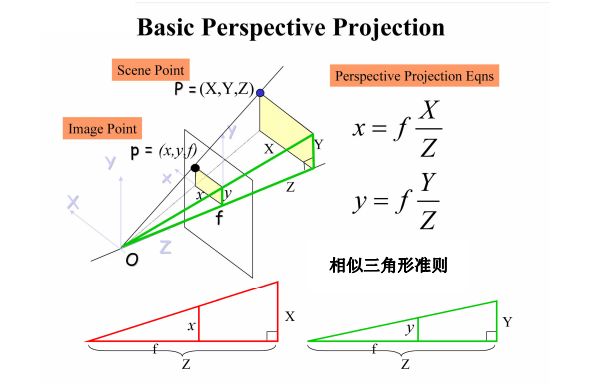

图像(物理)坐标系到像素坐标系
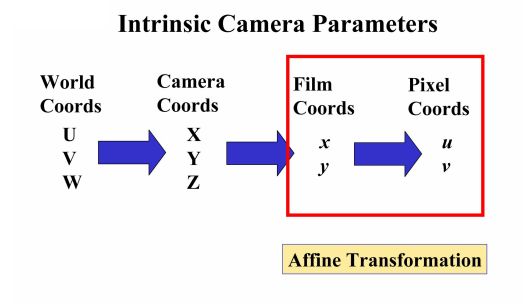

坐标系转换总览
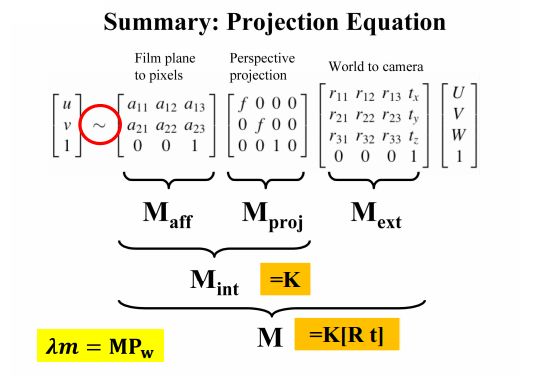
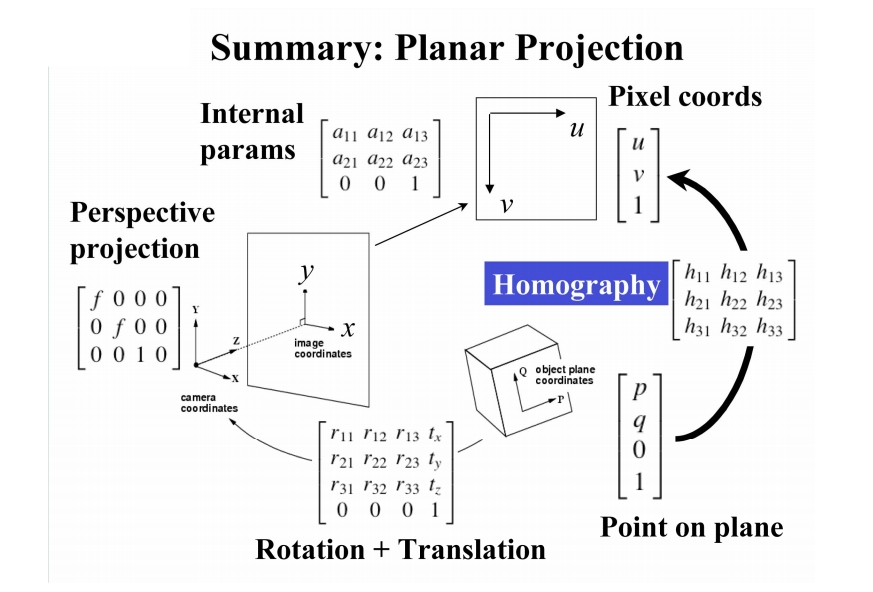
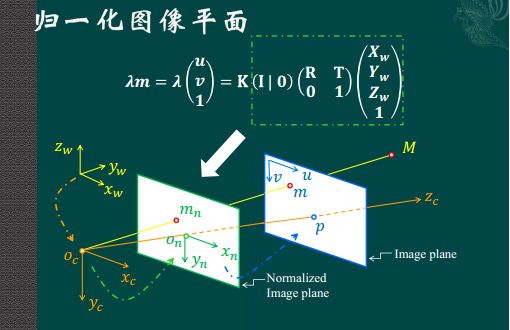
上图中,$\mathbb{K}$代表着摄像机的内参数(四~五个参数,两个缩放,两个平移,一个由于制造误差可能造成的摄像机坐标系歪斜角度),即摄像机坐标系和像素坐标系之间的关系,$[\mathbb{R} \;\, \mathbf{t}]$为外参数(六个参数,三个旋转,三个平移),即摄像机在世界坐标系里的位置和方向。
考虑制造误差歪斜角(另个坐标轴不完全垂直)的话,内参数矩阵可以表示为
\begin{equation} \mathbb{K}=\begin{bmatrix} \alpha & -\alpha \cot\theta & o_{x} \\ 0 & \frac{\beta}{\sin\theta} & o_{y} \\ 0 & 0 & 1 \end{bmatrix} \end{equation}
其中$\alpha=\frac{f}{s_{x}}, \beta=\frac{f}{s_{y}}$,$\theta$为歪斜角度。
整个参数矩阵可以表示为
\begin{equation} \mathbb{M}=\mathbb{K}[\mathbb{R} \;\, \mathbf{t}]=\begin{bmatrix} \alpha\mathbf{r}_{1}^{T}-\alpha\cot\theta\mathbf{r}_{2}^{T}+o_{x}\mathbf{r}_{3}^{T} & \alpha t_{x} -\alpha\cot\theta t_{y}+o_{x}t_{z} \\ \frac{\beta}{\sin\theta}\mathbf{r}_{2}^{T}+o_{y}\mathbf{r}_{3}^{T} & \frac{\beta}{\sin\theta}t_{y}+o_{y}t_{z} \\ \mathbf{r}_{3}^{T} & t_{z} \end{bmatrix} \end{equation}
其中$\mathbf{r}_{1}^{T},\, \mathbf{r}_{2}^{T},\, \mathbf{r}_{3}^{T}$是$\mathbb{R}$的三行,$t_{x},\, t_{y},\, t_{z}$是向量$\mathbf{t}$的坐标。
镜头畸变