写在前面
图像特征点匹配就是找到两幅图像中对应的特征点,在两幅图像中分别提取特征点并用描述子进行描述后,后面的问题就是如何找到一一对应的点对,也就是找到两组特征点集合中两两距离最近的特定点匹配对。在特征点输了不大的情况下(点集合大致小于2500对),进行简单的穷举搜索就可以,但当点对数量很大维度较高时,穷举的效率就回大打折扣,KD-Tree就是用来解决此种情形下的匹配问题。下面对KD-Tree的构建,KD-Tree的最近邻查询算法,改进的最近邻查询——BBF(Best Bin First)查询算法分别进行讨论。
KD-Tree的构建
KD-Tree是对数据点在k为空间划分的一种二叉树数据结构,每个节点表示的一个数据空间范围。它的构建过程是一个循环迭代的过程,假设数据的维度是D维,每次选择D维数据中方差最大的维度,以中间的数据进行划分(左子空间,右子空间),直到数据空间中只包含一个数据点。它的构建流程图如下:
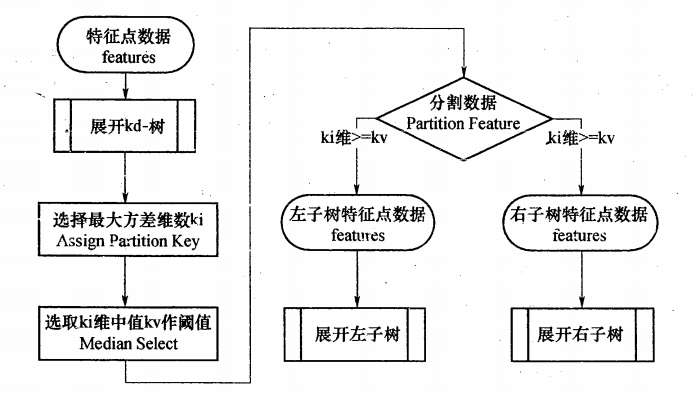
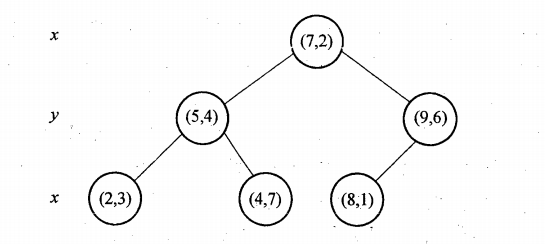
下面结合一个简单的例子加深理解,假设我们有6个二维数据点:$\{X,Y\}=\{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\}$,我们首先计算两个维度上的方差$(39,26.83)$。可见x维度上的方差大,方差越大说明此维度越容易区分,所以第一步是以x为分割域进行分割。将6个数据按x维度排序,选取中值数据$(7,2)$作为第一个分裂点对数据进行划分(x维度小于7的划到左边,大于等于的划到右边),得到两个子空间,然后对子空间按照上述步骤进行迭代划分,直到每个数据都划到根节点(节点数据空间只含有一个数据点)。示意图如下:
最近邻查询算法
在KD-Tree中进行数据查询是特征匹配的重要环节,目的是检测在KD-Tree中与查询点距离最近的数据点。查询过程可分为两步:二叉树搜索及回溯两步。
下面用文字简单下描述整个过程:
一、二叉树搜索
顺着路径找到最近邻的近似点,也就是与待查询点处于同一子空间的叶子节点(搜索过程可以概况为:比较待查询点与分裂点在分裂维度上的值,小于则划到左子空间,大于等于划到右子空间,迭代直至花到叶子节点)。
二、回溯
得到最邻近的近似点后(找到的叶子节点不一定是最近邻),沿上述搜索路径反向考察是否有距离查询节点更近的数据点(最近邻点肯定位于与查询点为圆心且通过最近邻近似点的园域内),直至回溯到根节点。K近邻查询类似最紧邻查询,只是将最近变为K个最近。
改进的最近邻查询——BBF查询算法
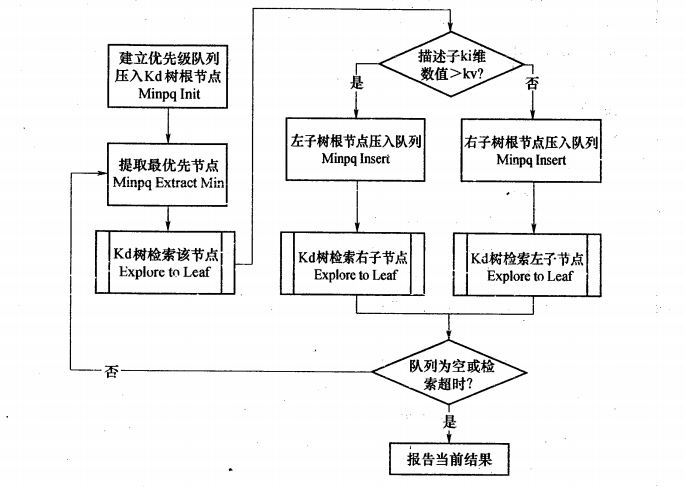
从上述标准的KD-Tree最近邻查询过程可以看出,起搜索过程的回溯是由搜索路径来决定,并没有考虑查询路径上数据点本身的一些性质。改进的查询算法——BBF(Best Bin First),通过将查询路径上的节点进行排序(如按各自分割超平面,也称Bin,与查询点的距离排序),优先回溯优先级最高(Best Bin)的节点来确保优先检索包含最近邻节点可能性更高的空间。BBF设置了一个运行超时限定,定优先级队列中的所有节点都经过检查或者超出时间限制时,算法返回目标找到的最好结果最为最近邻。下图是BBF整个算法流程:
小注
一、最近邻查询算法一般要求数据规模需要满足$N \gg 2^{D}$条件才能达到高效搜索。
二、最近邻查询算法维度不应超过20维。
三、改进的最近邻查询算法——BBF,可适用于高维数据。
四、BBF是以精度为代价来获取速度,其找到的最近邻不一定是最佳的。
五、在点集合2500以下时,穷举搜索时间效率更高。
参考文献
[1] 图像局部不变性特征与描述.王永明 王贵锦. 国防工业出版社.




