写在前面
图像配准对于运动平台(无人机,移动机器人)上的视觉处理有着极其重要的作用。配准算法的第一步通常是找到两幅图像中一一对应的匹配点对(特征点提取、描述、点对匹配),然后通过匹配点对求取变换矩阵。在图像特征点匹配之KD-Tree一文中讲了配准中第一步中的点对匹配方法,本文将集中讨论配准第二步。
在获得匹配点对后,我们需要从中选取一定的匹配正确的点对计算变换矩阵,对于透射变换,需要选取4组点对,对于仿射变换,需要选取3组。但现在的问题是,我们获得的匹配点对中不能保证所有的匹配都是正确的,如何从中选取正确的匹配点对来计算变换矩阵,这就需要利用下面要讲到的匹配对提纯的问题。
匹配对提纯算法可分为两类:比值提纯法与一致提纯法。比值提纯法就是在图像特征点匹配之KD-Tree一文中进行最近邻查询的时候,也对次近邻的距离进行查询,最后保留最近邻>=次近邻*THR(一般取THR=0.49)的匹配点对来进行提纯,不予细述。。下面将对一致提纯法进行详述,主要介绍常用的最小中值法(LMedS)、M估计(M-estimators)与随机采样一致算法(RANSAC)。
最小中值法(LMedS)
LMedS的做法很简单,就是从样本中随机抽出N个样本子集,使用最大似然(通常是最小二乘)对每个子集计算模型参数和该模型的偏差,记录该模型参数及子集中所有样本中偏差居中的那个样本的偏差(即Med偏差),最后选取N个样本子集中Med偏差最小的所对应的模型参数作为我们要估计的模型参数。
最小中值法可用数学表达简练的表达为:
$$\theta=arg_{\theta}\min med_{i \in N}r_{i}(x_{i},\theta)$$
$\theta$为拟合模型参数,$r_{i}(x_{i},\theta)$是模型第i个点的残留误差,N是我们随机抽出的样本子集,$med$为中值操作。
M估计(M-estimators)
对于含有外点的数据,如果对所有样本点使用一样的权重,在拟合模型时外点对模型会有较大的干扰,由此为出发点想到,如果降低外点的权重,则可以降低外点对模型的影响,这也就是M估计的一个思想。但问题是我们怎么知道哪些是外点呢,M估计中将与所估计模型偏差大的点视为外点,降低与模型偏差越大的点的权重。
一个M估计通过最小化下面的表达式来估计参数:
$$\theta=arg_{\theta} \sum_{i}\rho(r_{i}(x_{i},\theta);\sigma)$$
一般的为了降低偏差大的点的影响,$\rho(\mu,\sigma)$函数随着$\mu$的增加变平。常用的选择是:
$$\rho(\mu,\sigma)=\frac{\mu^{2}}{\sigma^{2}+\mu^{2}}$$
$\sigma$参数是控制函数变平点的变量,下图是当$\sigma^{2}=0.1, 1, 10$时画的$rho(x,\sigma)=\frac{x^{2}}{\sigma^{2}+x^{2}}$
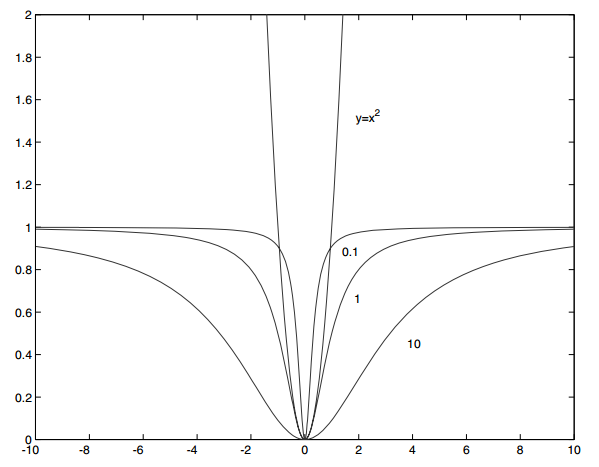
通过引入$\rho$,M估计可以保证外点作用被衰减的程度要比它们产生平方误差的程度要高。
从M估计的数学表达可以看出,问题是非线性的,必须迭代求解,下面是具体求解算法:
算法1 用M估计拟合概率模型参数
对于$s$从1到$k$
均匀随机抽取$r$个不同点组成样本子集
用最大似然(通常是最小二乘)对抽取的点集进行拟合获得$\theta_{s}^{0}$
用$\theta_{s}^{n-1}$估计$\sigma_{s}^{n-1}$,一个流行的估计式是:$\sigma^{n-1}=1.4826median_{i}|r_{i}^{n-1};\theta^{n-1}|$
直到收敛($|\theta_{s}^{n}-\theta_{s}^{n-1}|$非常小)
用最小化方法通过$\theta_{s}^{n-1},\sigma_{s}^{n-1}$得到$\theta_{s}^{n}$
计算$\sigma_{s}^{n}$
End
End
使用残差的中值作为准则获得这个集合的最好拟合,用最好拟合的参数作为模型的参数
随机采样一致算法(RANSAC)
M估计计算复杂性较高。另外一种最常用的方法是随机采样一致算法(RANSAC,Random Sample Consensus)。它的基本思路是随机选择一个小的数据点子集,然后对其进行拟合,查看有多少其他点匹配到拟合的模型上,迭代这个过程直至有较大的概率找到我们想要拟合的模型。
我们先看下RANSAC的算法流程,然后对其中的步骤进行详细阐述。
算法2 用随机采样一致(RANSAC)拟合概率模型参数
确定:
$n$——所需要的最少点数
$k$——需要的迭代次数
$d$——判断一个点是否拟合的很好的阈值,也称内外点距离阈值
$t$——判断一个模型是否拟合的很好所需要的邻近点数目,也称一致性集合大小阈值
直到$k$次迭代完成
从数据中均匀的采样$n$个点
对这$n$个点进行模型拟合
对于采样外的每个点
用$d$比较点到拟合模型的距离,如果距离小于$d$,则认为点是靠近的
End
如果有$t$个或者更多的点靠近模型,则认为该拟合是个好的拟合,重新用这些点和靠近的点拟合模型。
End
使用拟合误差最小的所对应的参数作为该模型的估计参数。
RANSAC的难点是$n,k,d,t$这几个参数的确定,下面就怎么确定参数做简单的讨论。
一、最少点数$n$的确定
相对比较容易,根据要拟合的模型确定。例,如果拟合一天直线,最少需要两个点;对于图片配准,拟合透射变换矩阵最少需要4组点对,拟合仿射变换,最少需要3组点对。
二、迭代次数$k$的确定
令$w$为数据是真实数学模型内点的概率,则一次估计中所有$n$个点(确定模型参数的最小点数)都为内点的概率为$w^{n}$。我们需要保证$k$次迭代中至少一次估计中所有数据点都是内点的概率$p$较大,则$k$需要满足:
$$1-p=(1-w^{n})^{k} \Rightarrow k=\frac{log(1-p)}{log(1-w^{n})}$$
其中$p$取一个较大的值。
三、内外点距离阈值$d$的确定
这个阈值用来判断数据点是内点或是外点,没有一个统一的方法,只能通过实验得到。
四、一致性集合大小阈值$t$的确定
令数据点集中外点的概率为$y$,我们需要选择$t$个点使得$y^{t}$很小(比如小于0.05)。$y$通常是无法精确的估计,如果真实模型中内点占优势,经过随机采样后$y$一般比$(1-w)$要小,即可由$y \le (1-w) $。
确定这些参数后就可以用RANSAC算法估计模型参数了。
小注
图像配准过程中匹配点提纯最常用的算法是RANSAC,其收敛速度快,在噪声点(外点)较多时也能有不错的表现。
参考文献
[1] 图像局部不变性特征与描述.王永明 王贵锦. 国防工业出版社.
[2] Computer Vision: A Modern Approach. David A. Forsyth and Jean Poince.




