写在前面
计算机视觉中很多问题都涉及到模型参数估计,例如给定两幅图像中的匹配点对来求取单应变换矩阵。最小二乘本质上是一种通过最小化均方误差来求取最优的模型参数的数据拟合方法。下文将依次介绍线性最小二乘、非线性最小二乘及它们的求解方法。
线性最小二乘法
假设有$p$个关于$q$个未知数的线性方程组:
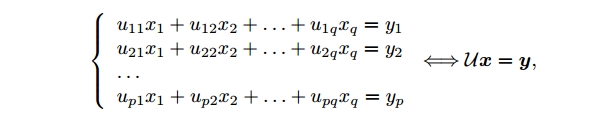
在这个方程组中令
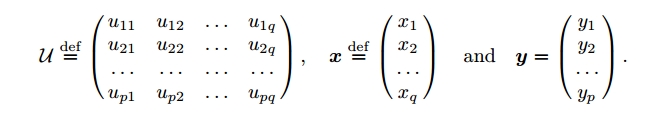
由线性代数理论可知:
当$p<q$时,方程的解集构成一个$(q-p)$维数的$\mathbb{R}^{q}$的子空间;
当$p=q$时,有唯一解;
当$p>q$时,方程无解。
当$\mathcal{U}$的秩(线性独立的行或列的最大数目)最大(等于$\min(p,q)$)时,以上结论成立。当秩小于$\min(p,q)$时,解的存在性取决于$\mathbf{y}$的取值以及它是否在$\mathcal{U}$构成的空间内(由各列张成的$\mathbb{R}^{p}$的子空间)。
正则方程和伪逆
本节剩余部分将假设$\mathcal{U}$是过约束的,即$p>q$,且秩为$q$。在这种情况下没有标准的解,只能找到使误差最小的向量$\mathbf{x}$,误差定义为
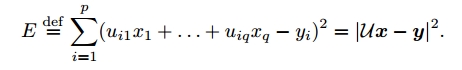
上式最小化均方误差即为最小二乘法。将误差写为$E=\mathbf{e}\cdot\mathbf{e}$,其中$\mathbf{e}\stackrel{\text{def}}{=} \mathcal{U}\mathbf{x}-\mathbf{y}$。为找到使$E$最小的$\mathbf{x}$,$\mathbf{x}$d 每一个分量的导数必须为0,即
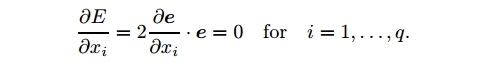
若$\mathcal{U}$的各列表示为$\mathbf{c}_{j}=(u_{1j},\cdots ,u_{mj})^{T}\;\;(j=1,\cdots , q)$,则有
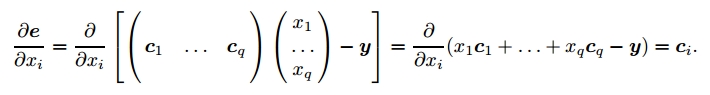
带入前式有
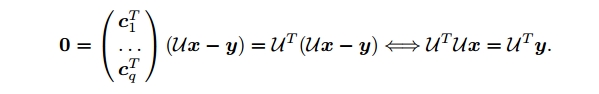
当$\mathcal{U}$满秩时,矩阵$\mathcal{U}^{T}\mathcal{U}$是可逆的,则方程$\mathbf{x}=\mathcal{U}^{\dagger}\mathbf{y}$(其中$\mathcal{U}^{\dagger}\stackrel{\text{def}}{=}(\mathcal{U}^{T}\mathcal{U})^{-1}\mathcal{U}^{T}$)的解就是所求的$\mathbf{x}$。$\mathcal{U}^{\dagger}$称为伪逆矩阵。在求解线性最小二乘法时,不一定要计算伪逆矩阵的实际值,一般通过QR或者SVD分解的方法来更快速的求解。具体求解步骤可以参考文献[2]。
齐次系统的求解
如果$\mathbf{y}$为0,则原始问题转换为了齐次系统的求解问题,即
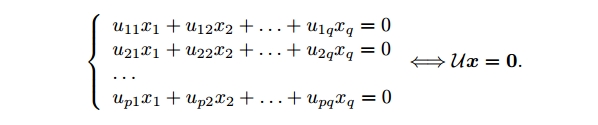
上式是关于$\mathbf{x}$的齐次方程。当$p=q$且矩阵$\mathcal{U}$非奇异时,上式有唯一解;当$p\geq q$且$\mathcal{U}$奇异时(秩小于$q$),方程才有非零解。此种情况下如果不引入附加限制,原始的误差最小化$E=|\mathcal{U}\mathbf{x}|^{2}$是没有意义的,因为总能让$\mathbf{x}$接近0来使得误差很小。由方程的齐次性,有$E(\lambda\mathbf{x})=\lambda^{2}E(\mathbf{x})$,因此要求$|\mathbf{x}|^{2}=1$是一个合理限制,避免没有意义的解并且可以得到唯一解。
误差$E$可以写成$|\mathcal{U}\mathbf{x}|^{2}=\mathbf{x}^{T}(\mathcal{U}^{T}\mathcal{U})\mathbf{x}$,其中$q\times q$的矩阵$\mathcal{U}^{T}\mathcal{U}$是半正定的,可以通过特征值分解过程对角化,特征向量为$\mathbf{e}_{i}(i=1,\cdots ,q)$,特征值为$0\leq \lambda_{1} \leq \cdots \leq \lambda_{q}$。任意单位向量$\mathbf{x}$可用这些特征向量表示为$\mathbf{x}=u_{1}\mathbf{e}_{1}+\cdots +u_{q}\mathbf{e}_{q}$,其中$u_{1}^{2}+\cdots +u_{q}^{2}=1$,则有:
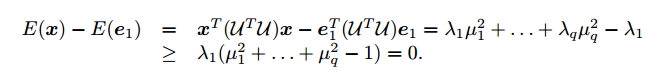
可以看出使$E$最小的$\mathbf{x}$即为$\mathcal{U}^{T}\mathcal{U}$的最小特征值对应的特征向量$\mathbf{e}_{1}$,此时得到最小误差$\lambda_{1}$。计算对称矩阵依旧可以用QR分解,SVD分解等多种方法,而不需要算出$\mathcal{U}^{T}\mathcal{U}$。
非线性最小二乘法
考虑一般情况下的$p$个方程和$q$个未知数:
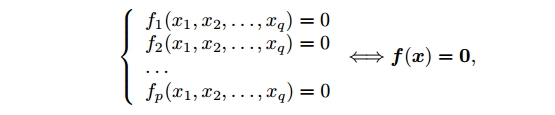
其中$f_{i}(i=1,\cdots ,p)$是$\mathbb{R}^{p}$到$\mathbb{R}$上的可微函数。用缩写$\mathbf{f}=(f_{1},\cdots , f_{p})^{T}$和$\mathbf{x}=(x_{1},\cdots , x_{q})$表示。一般情况下有
当$p<q$时,解构成一个$\mathbb{R}^{q}$上的$(q-p)$维的子集;
当$p=q$时,有有限个解;
当$p>q$时,方程无解。
这与线性情况有几处明显的不同:在欠约束的情况下,解的维数仍是$q-p$,但是不再构成一个向量空间,其结构由$f_{i}$决定。在$p=q$的情况下,不在是唯一解而是若干个。没有一个通用的方法可以找到上述方程在$p=q$的所有解或者$p>q$是的全局最小值解
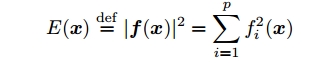
因此下面要介绍的是把原问题简化为局部线性问题的迭代方法,来力求找到至少一个合理解。它们都是建立在$\mathbf{x}$领域上$f_{i}$的一阶泰勒展开式基础上:
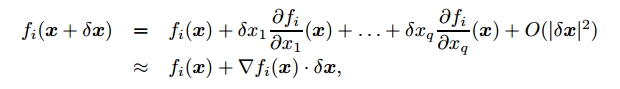
其中$\bigtriangledown f_{i}(\mathbf{x})=(\partial f_{i}/\partial x_{1}, \cdots ,\partial f_{i}/\partial x_{q})^{T}$是$f_{i}$在点$\mathbf{x}$的梯度值。在忽略二次项($O(|\delta \mathbf{x}|^{2})$)的情况下马上可以得到
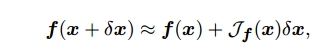
其中$\mathcal{J}_{f}(\mathbf{x})$是$\mathbf{f}$的Jacobian矩阵,定义为一个$p\times q$矩阵
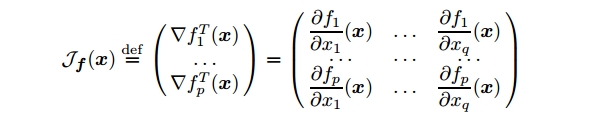
牛顿法:非线性方程的方阵系统
思想是:当$p=q$是,一般方法不能找到所有的解,但可以以$f(\mathbf{x}+\delta \mathbf{x})\approx f(\mathbf{x})+\mathcal{J}_{f}(\mathbf{x})\delta \mathbf{x}$为基础,构造一个迭代方法找到其中一个解。已知解的当前估计值为$\mathbf{x}$,对$\mathbf{x}$施加一个扰动$\delta \mathbf{x}$来使得$f(\mathbf{x}+\delta \mathbf{x})=0$,即
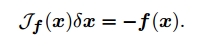
当这个Jacobian矩阵非奇异时,解上面的方程既可以找到$\delta \mathbf{x}$的合适解,重复这个过程直至收敛。牛顿法在接近解的地方收敛很快,按照平方速度收敛,但起始点离解很远时,上述牛顿法可能失败。
牛顿法:非线性方程的过约束系统
思想是:当$p>q$时,找到一个均方误差$E$的局部极小解。在极小值点,$E$的导数为零,利用这个特征来使用牛顿法。令$F(\mathbf{x})=\frac{1}{2}\bigtriangledown E(\mathbf{x})$,用牛顿法可以找到非线性方程组$F(\mathbf{x})=0$的一组解。由$E$微分可得到
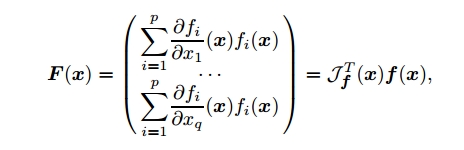
$F$的Jacobian矩阵就是:
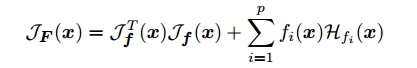
其中$\mathcal{H}_{f_{i}}(\mathbf{x})$是$f_{i}$的Hessian矩阵,由$f_{i}$的二阶导数组成
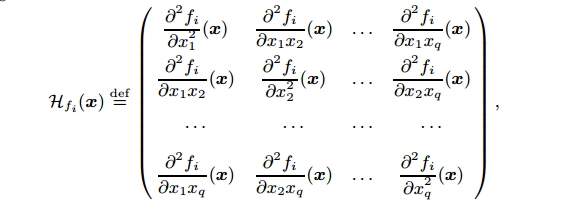
在牛顿法中,$\delta \mathbf{x}$满足$\mathcal{J}_{F}(\mathbf{x})\delta \mathbf{x}=-F(\mathbf{x})$,则可以推出
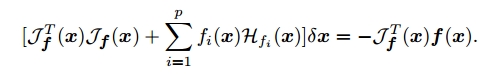
高斯牛顿法和Levenberg-Marquardt方法
牛顿法需要计算Hessians矩阵,不但困难而且耗时。下面介绍两种不需要计算Hessians矩阵的非线性优化方法:高斯牛顿法和Levenberg-Marquardt方法。
高斯牛顿法还是利用$\mathbf{f}$的一阶泰勒展开式逼近$E$的极小值。但对给定的$\mathbf{x}$,找到$\delta \mathbf{x}$使得$E(\mathbf{x}+ \delta \mathbf{x})$最小。
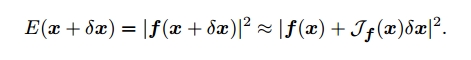
现在问题转化为了求线性最小二乘解的问题,$\delta \mathbf{x}$可以通过解线性方程或通过伪逆得到
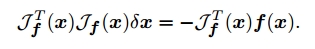
比较上式和非线性方程过约束系统的牛顿法可以看出高斯牛顿法是牛顿法的一种近似,其忽略了Hessians矩阵部分。当$f_{i}$在解的附近取值(残差)很小是这种近似是可以的。若残差很大,高斯牛顿法可能收敛很慢或者不收敛。
对上式稍加修改有
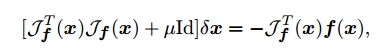
其中$\mu$在每步迭代可以取不同的值,此即为计算机视觉中常用的Levenberg-Marquardt方法。其用单位阵的倍数取代了包含Hessians的项。其和高斯牛顿法有相同的收敛速度,但是它更加鲁棒:即时在Jacobian矩阵$\mathcal{J}_{f}$不满秩以及伪逆不存在的情况下也能够使用。
小注
上文基本摘录整理自《计算机视觉-一种现代方法》第三章,感兴趣的同学根据参考文献进行延伸阅读。
参考文献
[1] Computer Vision: A Modern Approach. David A. Forsyth and Jean Poince.
[2] 求解最小二乘的几种方法
[3] 计算机视觉-一种现代方法. David A. Forsyth and Jean Poince.




