写在前面
本文将整理总结下射影几何中的欧式变换、相似变换、仿射变换、射影变换及多视角几何中的外极线约束、本征矩阵、基础矩阵及其估计等知识。
二维射影变换
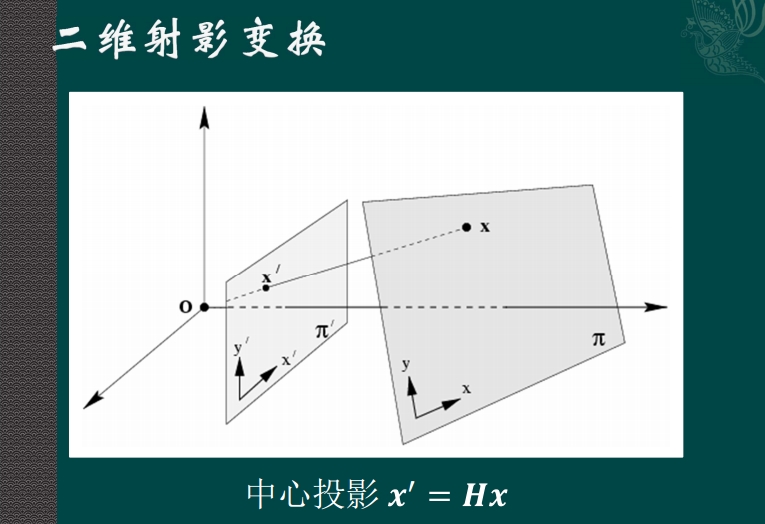
由摄像机成像的几何模型,可以看出被拍摄物体的成像过程实际是一个射影变换过程。
二维射影变换的定义

二维射影变换的层次
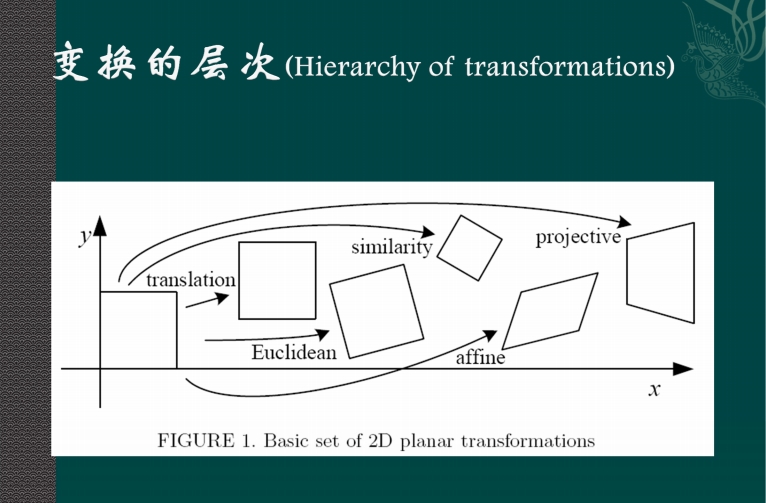
二维射影变换有欧式变换、相似变换、仿射变换、射影变换等几种层次。如下图所示:
基本变换形式的表示
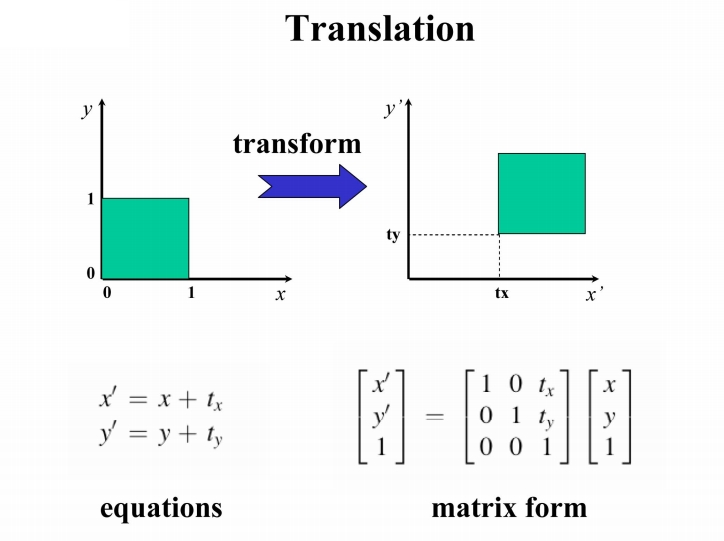
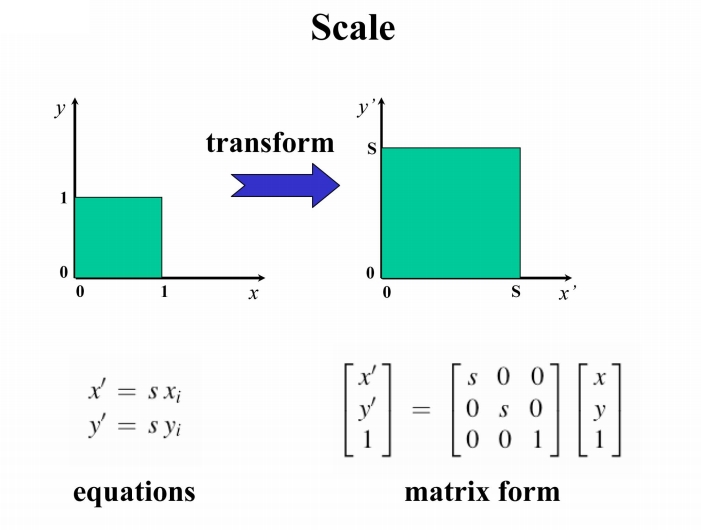
一般变换形式有平移、缩放、旋转三种,各个变换的示意图和数学表示如下;
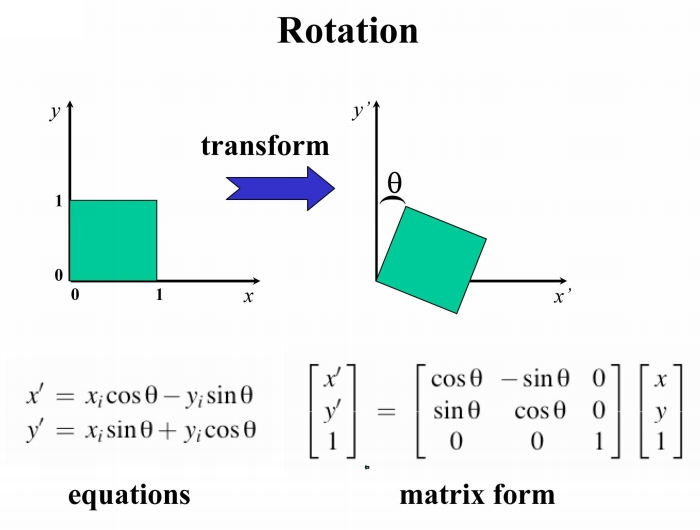
欧式变换
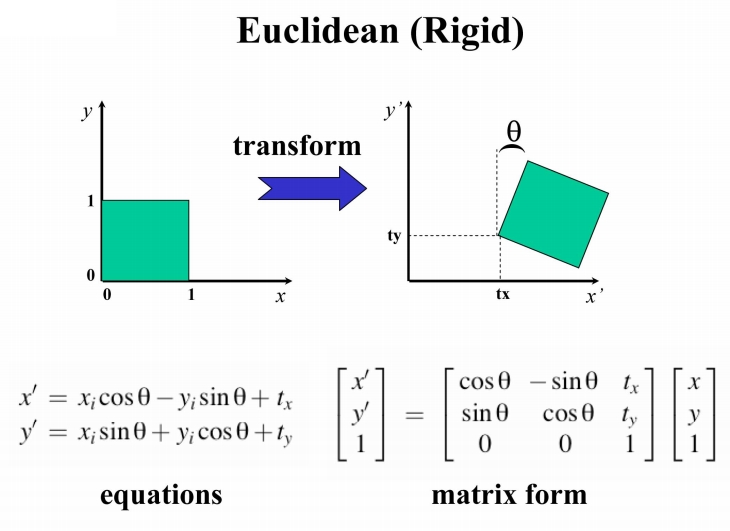

相似变换
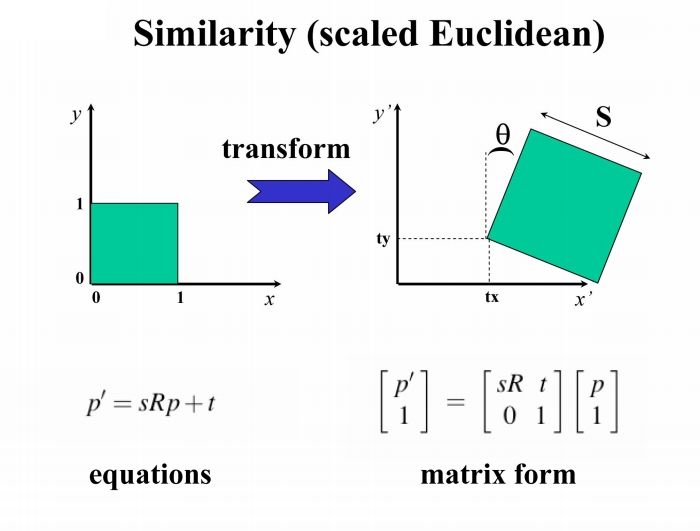

仿射变换
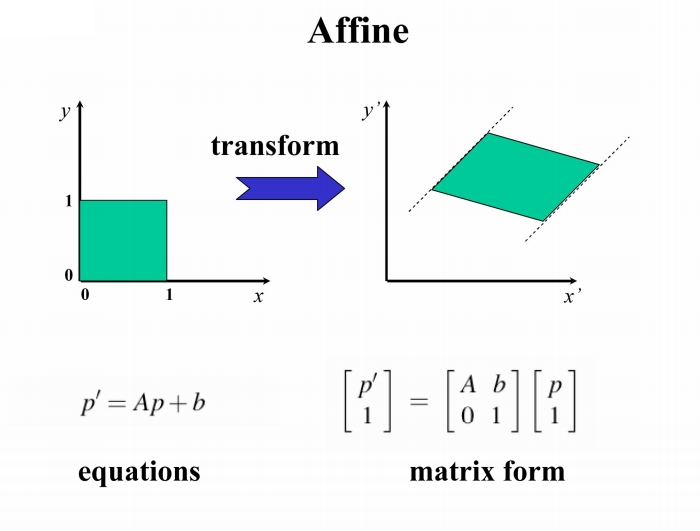
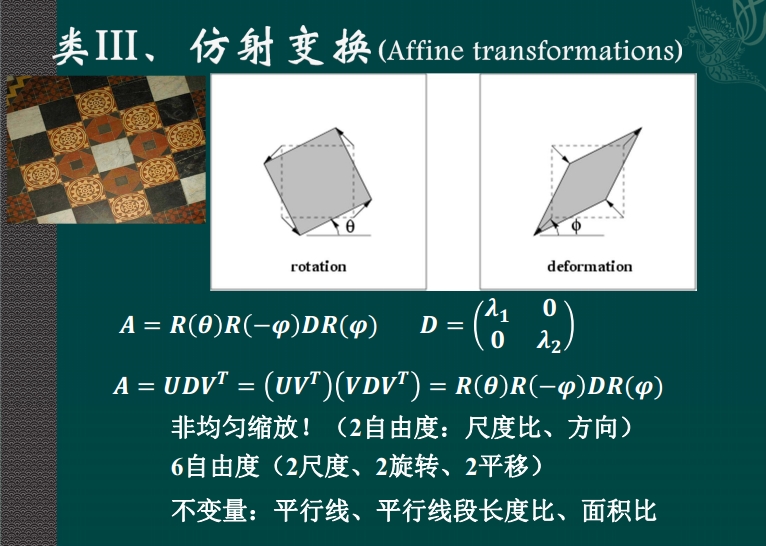
射影变换
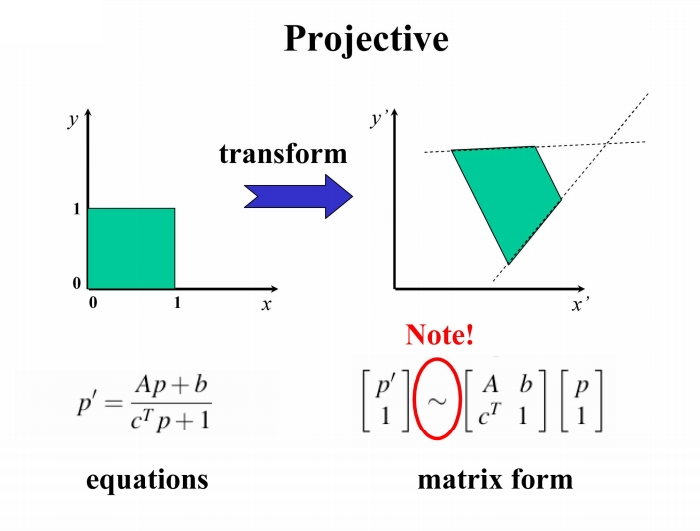

变换小结

求解单应变换矩阵




多视角几何
尽管图像中包含着丰富的信息,但是从一幅图像无法直接获得图像中物体的深度信息,需要由两幅或多幅不同视角拍摄的图像来获得。多视角几何就是研究这些图像之间的代数几何关系。下面主要介绍双目视角,从外极几何、本征矩阵、基础矩阵这几个点来介绍。
外极几何
下图是一个外极几何的示意图:
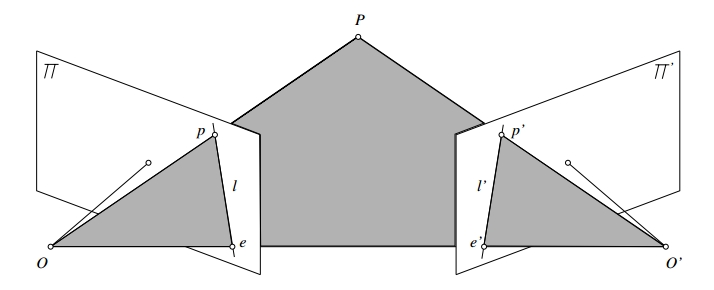
图中$P$是待观测点,$O$,$O'$是两台摄像机的光学中心,$p$和$p'$是$P$点所成的像。这5个点都位于两条相交光线$OP$和$O'P$所形成的外极平面上。两个光学中心的连线$OO'$称做基线,点$e$,$e'$称为两个摄像机的外极点,直线$l'$是与$p$关联的外极线,$l$是与$p'$关联的外极线。
对于$p$和$p'$这种同一个点的不同像点,$p'$一定位于与$p$相关联的外极线上,反之亦然,这种约束成为外极线约束。外极线约束在很大程度上限制了寻找两幅图像中点对应关系的搜索范围。
本征矩阵
如果假定每台摄像机的内部参数已知,可认为图像(物理)坐标系上的点$\mathbf{p}=\hat{\mathbf{p}}$,其中$\hat{\mathbf{p}}$代表像素点的坐标。显然,外极线约束说明了三个向量$\overrightarrow{Op}$,$\overrightarrow{O'p'}$和$\overrightarrow{OO'}$共面。等价地,其中一个向量在其他向量所在的平面上,即
$$\overrightarrow{Op}\cdot[\overrightarrow{OO'}\times \overrightarrow{O'p'}]=0$$
使用与第一台摄像机相关联的坐标系可以将上述与坐标无关的方程改写为
$$\mathbf{p}\cdot[\mathbf{t}\times (\mathbb{R}\mathbf{p}')]=0$$
其中$\mathbf{t}$是区分两个坐标系的坐标平移向量$\overrightarrow{OO'}$,$\mathbb{R}$是旋转矩阵,即在第二个坐标系统中坐标为$\mathbf{w}'$的自由向量在第一个坐标系中的坐标为$\mathbb{R}\mathbf{w}'$。
上式可以最终写为
$$\mathbf{p}^{T}\varepsilon \mathbf{p}'=0$$
其中$\varepsilon=[\mathbf{t}_{\times}]\mathbb{R}$,$[\mathbf{t}_{\times}]$表示斜对称矩阵,$[\mathbf{t}_{\times}]\mathbf{x}=\mathbf{t}\times \mathbf{x}$是向量$\mathbf{t}$和向量$\mathbf{x}$的叉积。
矩阵$\varepsilon$即是本征矩阵,坐标向量$\varepsilon^{T}\mathbf{p}(\varepsilon\mathbf{p}')$代表了再第二幅图像中与点$p(p')$关联的外极线。
本征矩阵($3\times 3$)可以通过旋转矩阵$\mathbb{R}$的3个自由度和决定平移向量$\mathbf{t}$的恋歌自由度来参数化,即其有5个自由度。
基础矩阵
实质上基础矩阵和本征矩阵是一种性质的,只是基础矩阵是在不知道摄像头内部参数信息推导出来的。当内部内部参数未知时(非标定的摄像机),可以写成$\mathbf{p}=\mathbb{K}^{-1}\hat{\mathbf{p}}$和$\mathbf{p}'=\mathbb{K}'^{-1}\hat{\mathbf{p}}'$。其中,$\mathbb{K}$和$\mathbb{K}'$是$3\times 3$的标定矩阵。则有:
$$\mathbf{p}^{T}\mathbb{F} \mathbf{p}'=0$$
上式中的矩阵$\mathbb{F}=\mathbb{K}^{-T}\varepsilon \mathbb{K}'^{-1}$即为基础矩阵。类似本征矩阵,基础矩阵也是提供了三维点到二维的一个约束条件,即:$\mathbb{F}\mathbf{p}'(\mathbb{F}^{T}\mathbf{p})$代表了再第一(二)个像中的点$\mathbf{p}'(\mathbf{p})$对应的外极线。
基础矩阵同样也是$3\times 3$的矩阵,同本征矩阵一样秩为2,秩为2的限制意味着基础矩阵只允许有7个独立的参数(自由度为7,因为相差一个常数因子和行列式值为0减掉两个自由度)。利用本征矩阵和相机内参数矩阵相乘可以得到基础矩阵。
弱标定
弱标定就是通过两幅图中冗余对应点集合来估计外极几何(基础矩阵估计)。
将上文中$\mathbf{p}^{T}\mathbb{F} \mathbf{p}'=0$写为
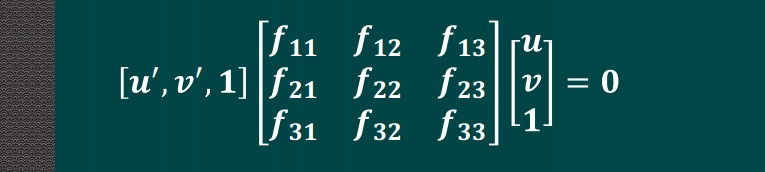
进行展开变换可得

可以看出,由对应的8组点对即可得到基础矩阵。和由两幅图像的匹配点对求解变换的单应矩阵不同(每一组点对可以展开为两个线性约束方程),其每组对应点只能展开为一个线性约束方程,所以弱标定至少需要8组对应点(单应变换矩阵虽有8个自由度但只需要四组)。
小结
本文整理自模式识别重点实验室的上课课件、计算机视觉-一种现代方法及计算机视觉的多视角几何。结合摄像机成像的几何模型进行阅读会更好的理解。
参考文献
[1] 模式识别重点实验室上课课件
[2] Computer Vision: A Modern Approach, Second Edition, David A. Forsyth and Jean Ponce
[3] Multiple View Geometry In Computer Vision, Second Edition, Richard Hartley and Andrew Zisserman




